집으로
제목: 집으로
번호: 1069
푼 날짜: 2024-02-04
문제는 여기에서 확인 가능합니다.
문제 내용 보기 (click me!)
문제
은진이는 지금 (X, Y)에 있고, (0, 0)에 있는 집으로 가능한 빨리 가려고 한다. 이동할 수 있는 방법은 다음 두 가지이다.
첫 번째 방법은 걷는것이다. 걸을 때는 1초에 1만큼 움직인다. 두 번째 방법은 점프하는 것이다. 점프를 하게 되면, T초에 D만큼 움직인다. 점프는 일직선으로만 할 수 있고, 정확하게 D칸만 움직일 수 있다.
위의 두 가지 방법을 이용해서 집에 돌아오는데 걸리는 시간의 최솟값을 구하는 프로그램을 작성하시오. 꼭 한 가지 방법만 사용해야 되는것이 아니고, 두 가지 방법을 적절히 조합해서 가장 빠른 시간을 구하는 것이다.
입력
첫째 줄에 네 정수 X, Y, D, T가 주어진다.
출력
첫째 줄에 집에 돌아오는데 걸리는 시간의 최솟값을 출력한다. 절대/상대 오차는 10-9까지 허용한다.
제한
- 1 ≤ X, Y ≤ 1,000
- 1 ≤ D, T ≤ 10,000
예제
입력 1
6 8 5 3
출력 1
6.0
입력 2
3 4 6 3
출력 2
4.0
입력 3
318 445 1200 800
출력 3
546.9451526432975
입력 4
400 300 150 10
출력 4
40.0
입력 5
6 8 3 2
출력 5
7.0
입력 6
10 10 1000 5
출력 6
10.0
풀이
import math
X, Y, D, T = map(int, input().split(' '))
a_square = X ** 2
b_square = Y ** 2
c_square = a_square + b_square
root_of_c = math.sqrt(c_square)
min_time = root_of_c
if root_of_c % D == 0:
min_time = min(min_time, root_of_c / D * T)
if (root_of_c + 1) % D == 0:
min_time = min(min_time, ((root_of_c+1) / D * T) + 1)
if (root_of_c - 1) % D == 0:
min_time = min(min_time, ((root_of_c-1) / D * T) + 1)
jump_count = root_of_c // D
remain_dist = root_of_c - (jump_count * D)
if jump_count > 0:
min_time = min(min_time, remain_dist + jump_count * T)
min_time = min(
min_time,
(((jump_count+1) * D) - root_of_c) + (jump_count + 1) * T
)
if (root_of_c > D):
min_time = min(min_time, (root_of_c // D) * T + T)
if (root_of_c < D*2):
min_time = min(min_time, T*2)
print(min_time)
언어: Python
알고리즘: 애드 혹, 기하학, 많은 조건 분기
난이도: GOLD 3
문제 해설
X,Y 에서 0,0 으로 가장 빠르게 이동할 수 있는 방법을 찾는 문제이다.
하지만 일반적인 문제였다면 당연히 대각선으로 이동하는게 빠를 것이다.
이 문제는 거기에 ‘점프’를 해서 더 빠르게 이동할 수 있는 방법이 있나 확인하고
가장 짧게 이동하는 경우를 찾으면 된다.
1만큼 이동하는데 1만큼이 시간이 걸린다. (그럼 0.9 를 이동하면 0.9 가 걸리는것이다.)
점프는 직선상으로밖에 움직이지 못한다. (즉 곡선으로 이동을 못한다.)
아래와 같은 경우를 모두 고려해줬다.
- 대각선으로 이동하는 경우.
a_square = X ** 2 b_square = Y ** 2 c_square = a_square + b_square root_of_c = math.sqrt(c_square) min_time = root_of_c- 대각선 길이를 구해서 최단거리를 구할 수 있다.
- 점프로만 갈 수 있는 경우
if root_of_c % D == 0: min_time = min(min_time, root_of_c / D * T)- 1 ≤ X, Y ≤ 1,000
- 1 ≤ D, T ≤ 10,000
- 제한이 위와 같으므로, 점프로만 가는 경우를 계산해도 최소한 대각선으로 가는것보다 같거나 오래걸리지 않는다.
- 점프로 이동했는데 1이 차이나는 경우들
if (root_of_c + 1) % D == 0: min_time = min(min_time, ((root_of_c+1) / D * T) + 1) if (root_of_c - 1) % D == 0: min_time = min(min_time, ((root_of_c-1) / D * T) + 1)
- 점프로 이동하고 남은거리를 걸어가는 경우들
jump_count = root_of_c // D remain_dist = root_of_c - (jump_count * D) if jump_count > 0: # 점프 하고 남은거리 걸어가는 경우 min_time = min(min_time, remain_dist + jump_count * T) # 뒤로 넘어가서 점프하고 걸어가는 경우 min_time = min( min_time, (((jump_count+1) * D) - root_of_c) + (jump_count + 1) * T )
- 최단거리로 안가고 점프로 가는 경우
if (root_of_c > D): min_time = min(min_time, (root_of_c // D) * T + T)- 점프로 이동할 수 있는거리 D 가 최단거리보다 작다면,
- 최단거리로 안가고 점프로 가는 경우는 아래 이미지처럼 갈 수 있을 것이다.
- 이 경우는 최단거리를 D 로 나눗 횟수 + 1번을 더 이동하게 된다.
- (그게 최소일 것이다)
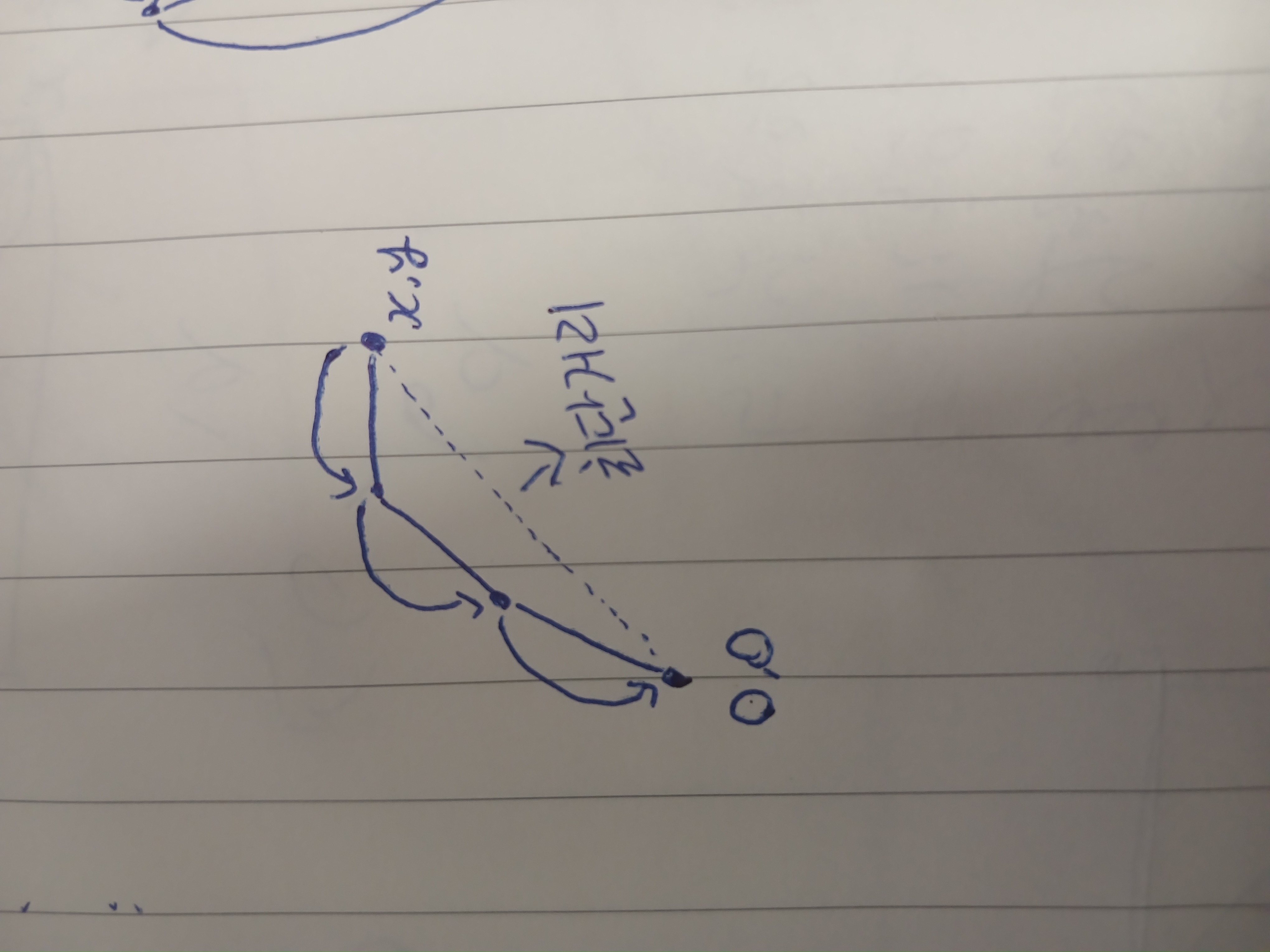
- 점프 두번으로 이동하는 경우
if (root_of_c < D*2): min_time = min(min_time, T*2)- 점프 2번으로 이동하는 거리보다 최단거리가 짧다면,
- 아래 이미지처럼 2번으로 이동할 수 있다.
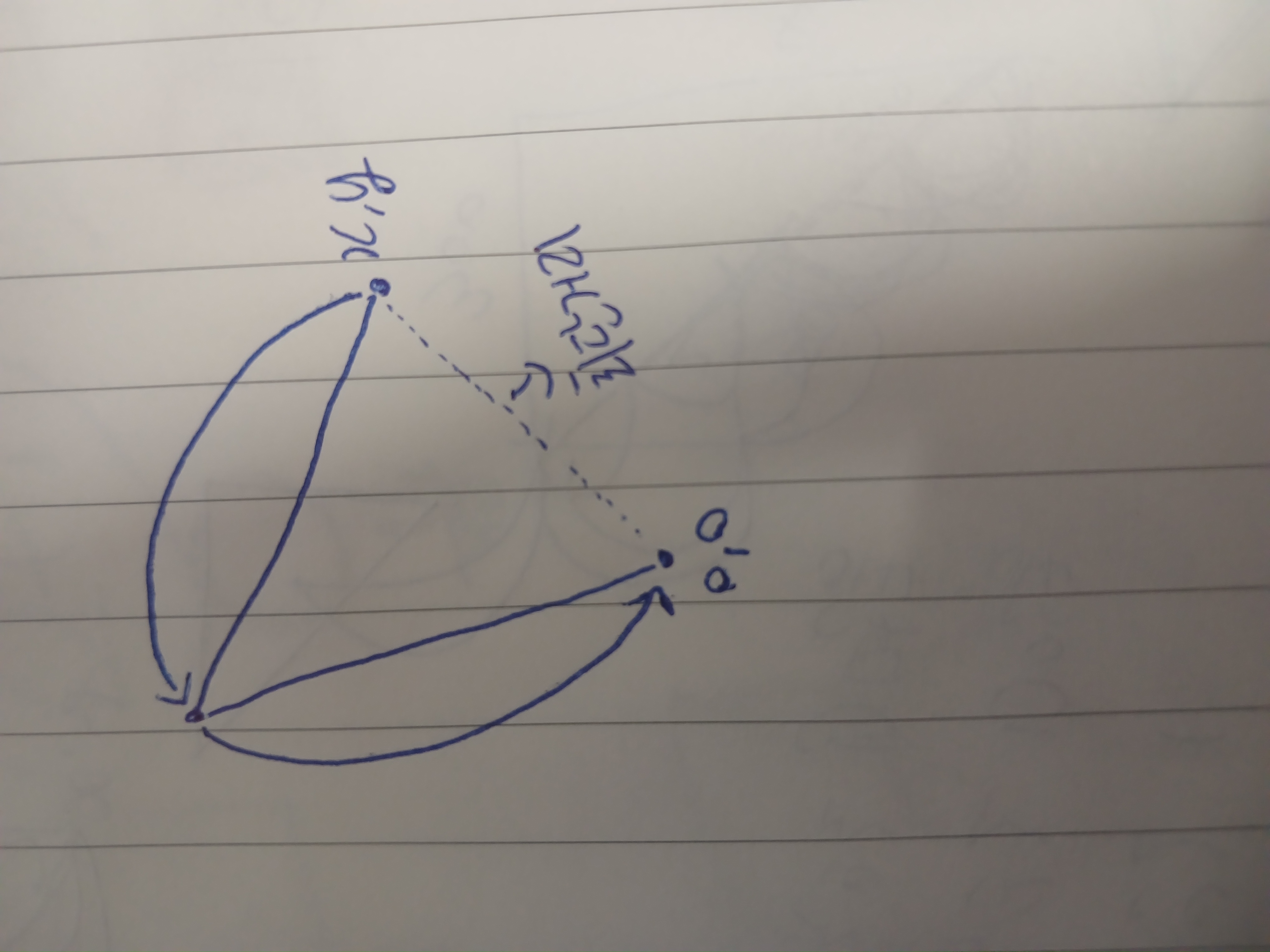
시간 복잡도의 경우 그저 수식 계산이라 따로 계산할 필요는 없었다.
위 경우를 모두 계산해줬고 통과했다. 